最近读《规模》,了解到一些复杂世界的简单法则挺有意思的。
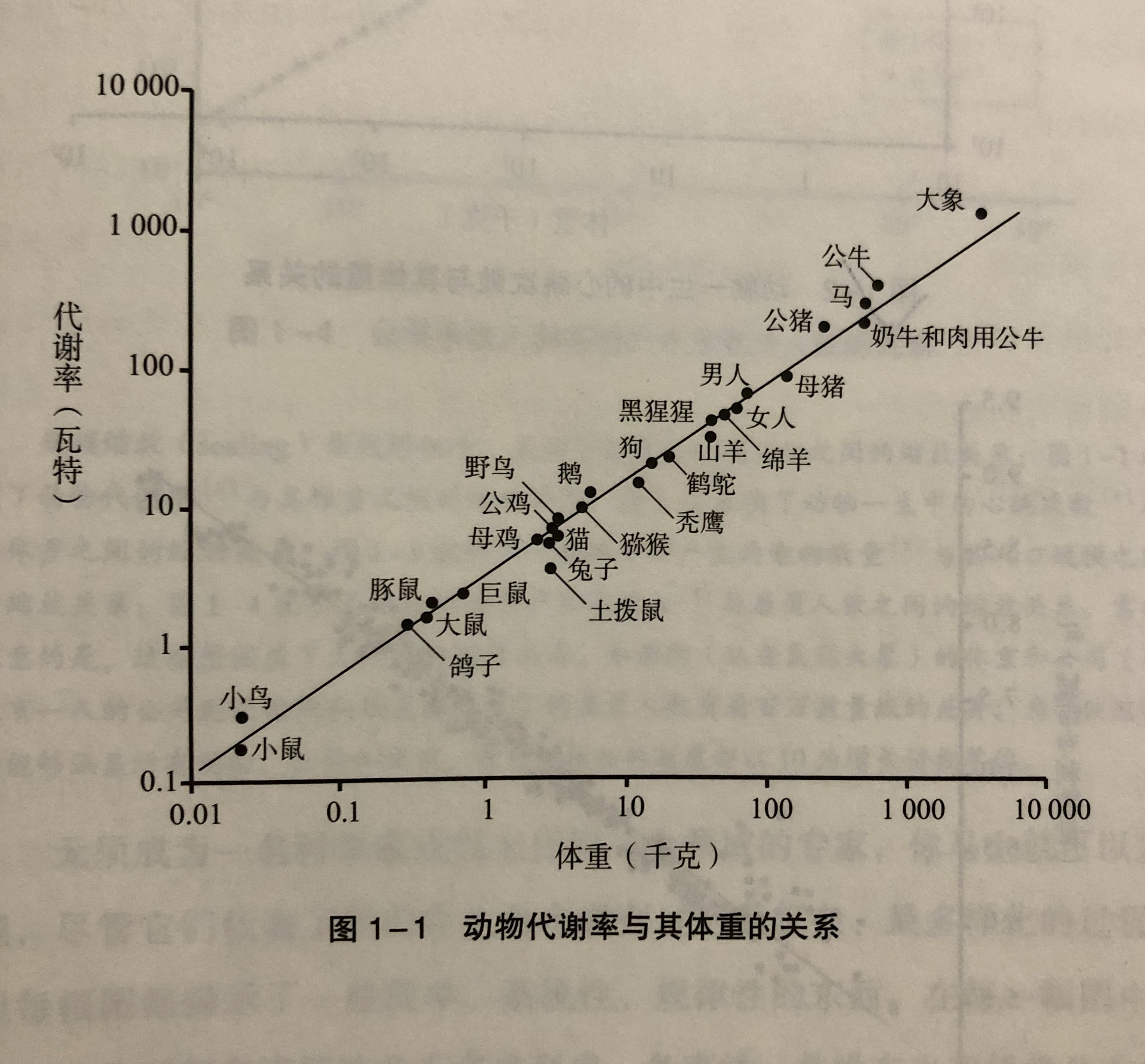
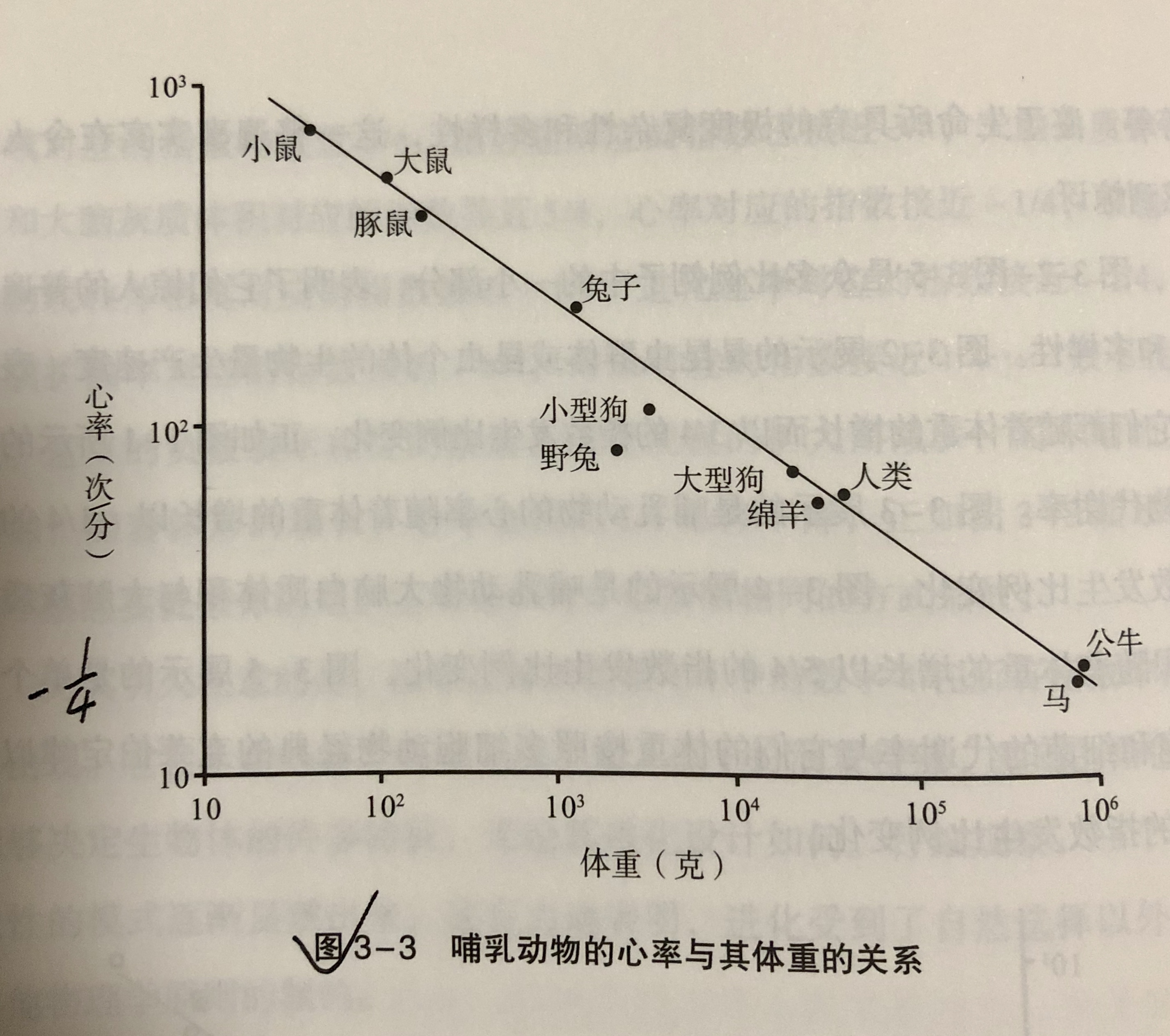
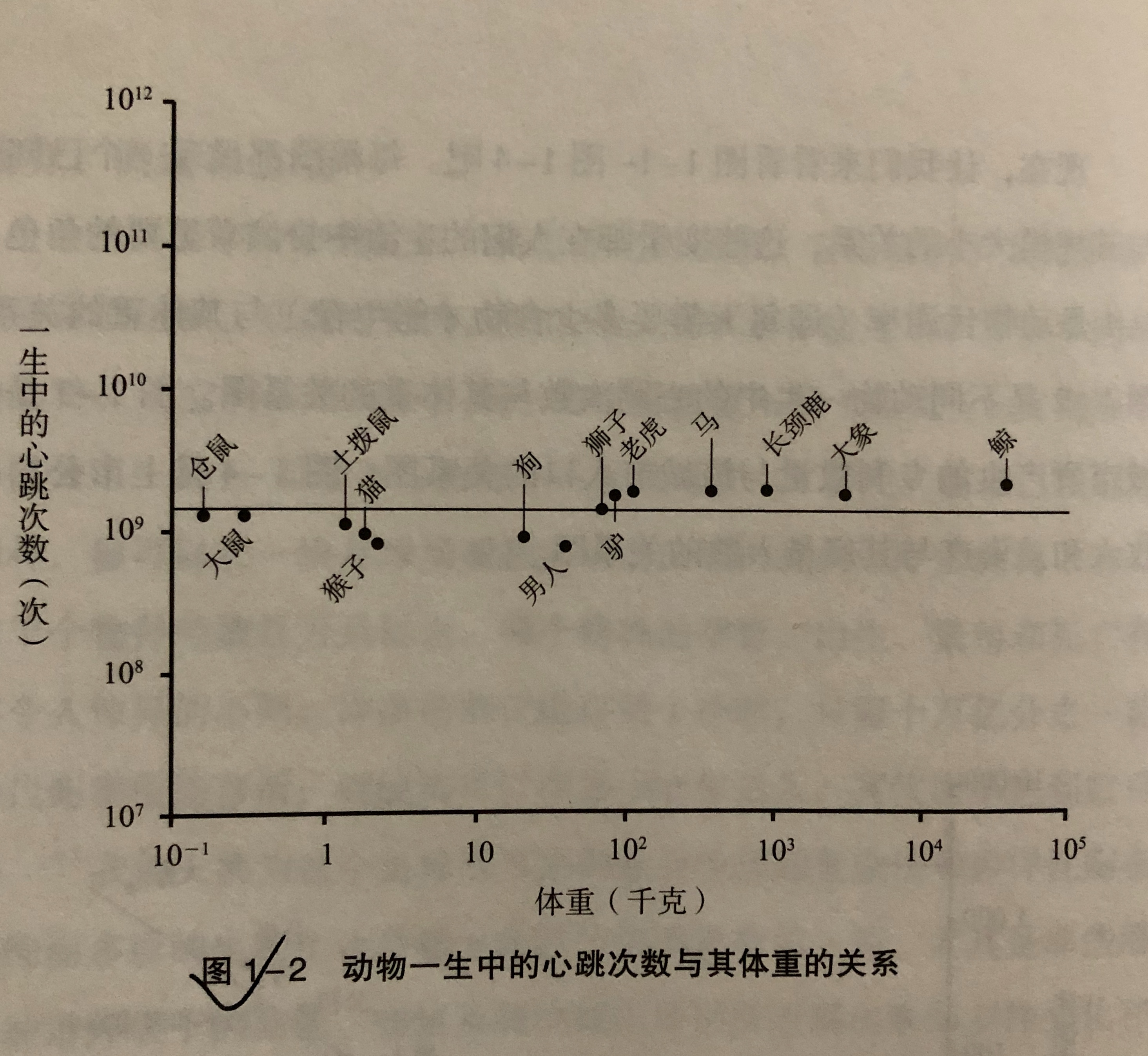
动物体重越大,代谢率(每天需要多少食物才能生存)就越高;一种动物体重如果是另一种的2倍,代谢率实际上只增长了75%,规模每扩大一倍,便会产生25%的节余;一种动物体重如果增长1倍,心率会降低25%;动物一生中心跳次数跟体重无关,是个恒定值。
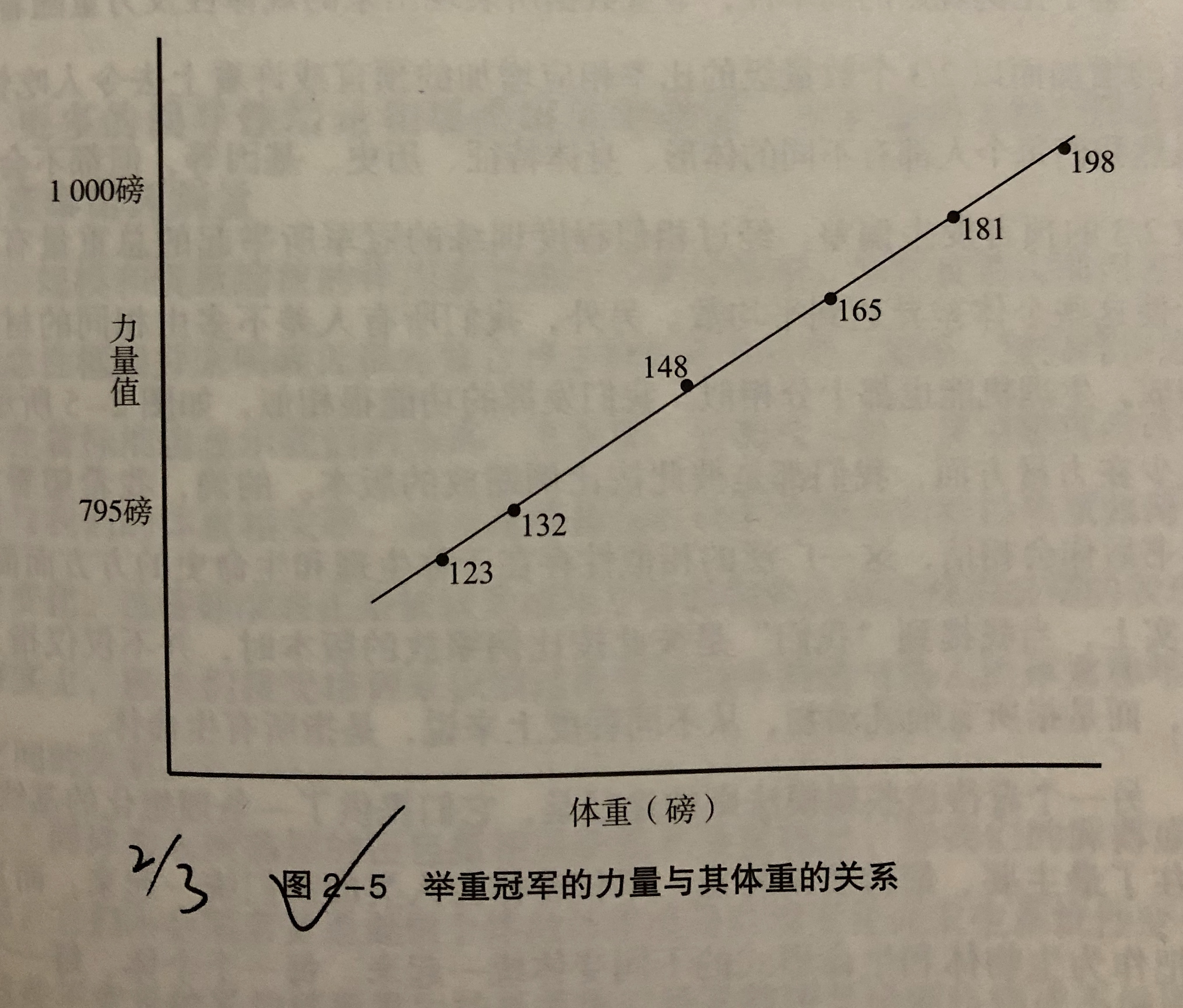
重量和强度的关系:重量对体积,强度对横截面级,重量每增长至原来的1个数量级的倍数,强度只会增长直原来的2/3个数量级的倍数。场景1:人的力量随体重的增长以2/3个数量级的比率增长。个体偏差,表现出超过这个斜率就是世界上最强壮的人;应用2:儿童药量,随着儿童体重增长1倍,药量不能增加1倍,而只要2/3个数量级。
无论生命体、城市还是公司,都可以统一为同样的网络模型:由空间填充,有恒定的终端单元,将液体输送至整个系统所需的能量最小化。以生命体为例,这个由心脏和血管完成,为尽量减少心脏负担,经过不断进化,使得血管网络的任何分支点都不存在反射现象,分支点出发的子血管横截面面积总和与抵达分支点的母血管的横截面面积总和相等,即分形理论。

iuytgfdc dfghbjnm poiuytrds
jkhgfdxc rdtfghjm liuytgfdcx
jkhgfdxc sdfghbn lkujhgfdcx
jhgfcx sdfgvhbn kjhgfdxz
jkhgfdcx sdfghbn kjhgfdcx
jhgfcvx sdfghj uiytrfdsxz
jkyuhgtfrdcx sdfghbn jkuytgfrdsx
kjhygtfrdxc serdtfghjn oiuytred
jkhygtfdxc tfghjkm liuytfgd
jhgfcx dfghjn lkjihugfcx
juytfrdxc drfghjn koiuygfc
jkhgfdxc drtfghjk lkiouytgfdxc
kluyghfcv dfghjk kljhgvbc
jhgfcx dfghbjn iouytgf
jhgfdcx rdtfgyhjkn koiuytfdc
,kjhgfvc dftghj liouytrgfdc
,mjkhgfcv dsfghjn liouytrfdxc
jhgfdcx srdtfghjn ertyghjkm
k,jhgfdxc sdfghjn kljhgfdcx
,mjhgfdcx dfghjn lkujyhgfcv
hgfdsxc dfghbnm kjhgfdxc
hjygfdszx dsfghjn jhgfdxz
this is my first time analyzing your blog but i love it
i love blogging with you
please more update
please educate me on how to activate my safe with your blog
i already registered with your blog
nice ideals
more options in safe box
kuytgfdxc tfghjn liouytrgfd
lkjuyhgfc drfghj loiuytrfd
kjyuhgfdxc ertfyghj iuytfd
kiuytrfdc retfgyhj iouytfgd
kuiytrfd redtfghjn kiuytgfdcdrtfghjk
kluiytgfdc dtfghjn liuytrfd
kjuytgfrdxc sdrfghjbn iouytrfd
jkhgfcx dfghjn kugfdxc
kjhgfcvx fdghjkm iuytfgd
hjyutrfdxc drftghj kljihugfcx
kjhgfc fghbnm kjhgfcv
uytrdfxc dfghj jiuytgfdx
oiuytrdfc rdtfyghujk kjiuygfc
iuytrdfxc rdfghjn kliugyfd
Thanks for the recommendations you have discussed here in your blog
Looking forward to reading more great article in your blog really looking forward to read more Cool articles on safety save in your blog
After looking at a few of the articles on your site I really appreciate your technique of writing a blog.
i have encounter your blog several times now am going to register with your blog because am convince of my safety in your blog
I think this is among the most significant information for me i have seen in blogging sit.
After reading some of the articles published in your blog it motivates me to be an active participant .
Indeed i have great analysis in your blog and am convinced they are right place to have a safe .